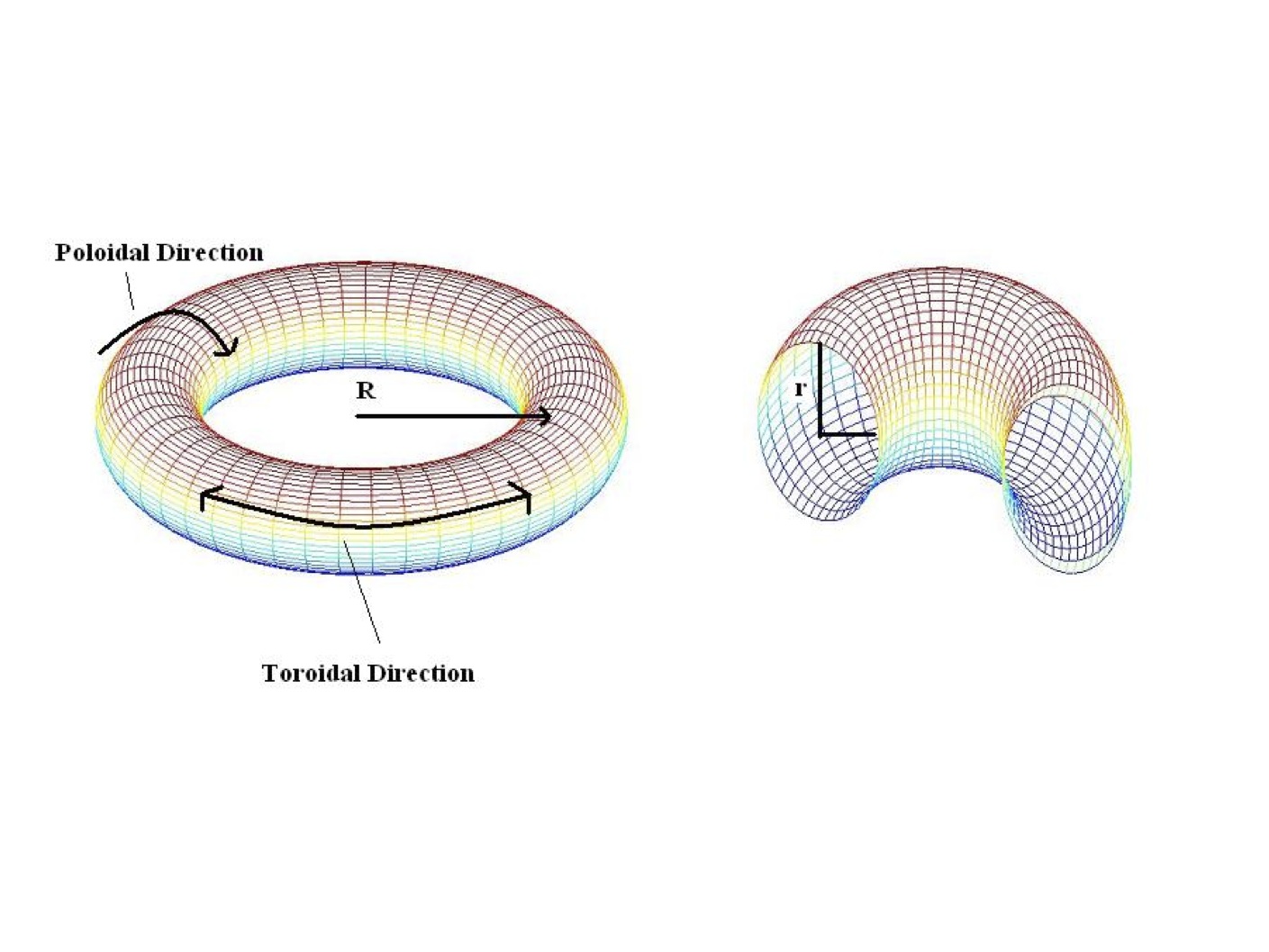
Magnetohydrodynamics Island Coalescence This models an instability in a reduced 2D tokamak model. Here, we look at a thin annulus in the cross section of a large-aspect ratio tokamak. The magnetic field in the toroidal direction (going around the torus) is large and mostly constant. Therefore, we only consider the instabilities in the poloidal direction. An initial equilibrium is perturbed resulting in two peaks of current density coalescing together. The result is a reconnection of magnetic field lines and sharp spike in current density at the reconnection point. The following movies show this for a variety of parameters. R = Reynolds Number S = Lundquist Number

3D Parallel Results (simulations by Lei Tang on Frost: IBM Blue Gene/L, formerly at NCAR) Current Density: R = S = 5,000     dt = 0.1     256 processors Current Density: R = S = 10,000   dt = 0.1     256 processors Current Density: R = S = 25,000   dt = 0.025 1024 processors Current Density: R = S = 50,001   dt = 0.025 1024 processors

2D Serial Results (Contour Plots) Current Density: R = S = 5000 With Adaptive Refinement Current Density: R = S = 10000 With Adaptive Refinement Current Density: R = S = 25000 With Adaptive Refinement Current Density: R = S = 50001 With Adaptive Refinement

Two-Phase Flow In these experiments, we use the diffusive interface theory to model the interaction of two fluids. The two fluids are distinguished from each other by introducing a phase-function. In the diffusive mixing region, the phillic and the phobic forces compete either to bring the two fluids together or to keep them separated. Depending on the parameters of the problem, the inherent energy laws will govern the behavior of the two fluids.

	Osculating Bubbles: 2 Bubbles of Fluid 1 Immersed in Fluid 2 Phase Function: with adaptive refinement and same viscosities		Square to Circle: 1 Bubble of Fluid 1 Immersed in Fluid 2 Phase Function: with adaptive refinement and same viscosities
	Varying Viscosity in L-shaped Bubble Phase Function: Viscosity in bubble 50 times outside. Phase Function: Viscosity in bubble 50 times outside plus shear flow.		Bubble in Pipe Phase Function: Bubble in long tube Mesh File: Bubble in long tube

Liquid Crystals Nematostatics In these experiments, we study various phenomena in static liquid cyrstal test problems. We look at varying parameters that affect the splay, twist, and bend of a liquid crystal configuration. In addition, we introduce a static electric field with and without a polarizing effect to see how the configuration changes. In all cases, we assume the liquid crystal is made up of cylindrical rods that can point in any direction, but only vary in the 2D plane and have length 1. We test how well a least-squares finite element approach does in solving such systems. The vector fields of the rods are displayed in the following movies. Here, the parameters K1, K2, and K3 represent the twist, splay, and bend Frank constants of the overall configuration.

	Nematics K1=1, K2=1, K3=1 K1=1, K2=0.5, K3 = 1.5 K1=1, K2=0.25, K3 = 1.5 K1=1, K2=0.1, K3 = 1		Banana Crystals K1=1, K2=0.5, K3=0.5 K1=1, K2=0.5, K3=0.25 K1=1, K2=0.5, K3=0.1 K1=1, K2=0.5, K3=0.01
	Electric Field Added No Polarization Effect Top Voltage = 2, K1 = 1, K2 = 0.63, K3 = 1.32